代谢组学的生物信息学分析
生物信息学数据处理的基本原则是将原始数据文件转换成可以轻松解读的参数,包括离子保留时间,m/z,以及每个原始数据文件中的离子强度测量值等等。除了这些基本特征以外,数据处理还可以提取其他信息,如离子的同位素分布。
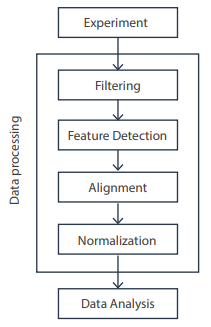
数据处理一般流程
单变量分析
代谢组学数据通常是多维的,特征(峰、代谢物)的数量从几十个到几百个甚至数千个不等。所采集数据的特征代表了每种生物的生化特征的快照。这些特征中的大多数都在正常生理范围内,而有些可能由于生理条件的变化而显著波动。鉴定这些“关键”特征是发现潜在生物标志物并揭示其潜在生物学功能的第一步。常见的单变量分析包括:
1. 倍数变化分析
倍数变化(Fold change, FC)是描述最终值与原始值之间定量变化程度的度量。FC可以用来分析蛋白质组学和代谢组学中的基因表达数据,以测量不同条件下表达量的变化。FC法的缺点是存在偏差,可能会丢失差异较大(YX)但比率较小(X/Y)的差异表达基因,导致高强度率下的高缺失。
2. T-检验
T检验可以用来确定两个数据集之间是否存在显著差异。单样本t检验用于检验样本平均值与已知总体平均值之间的差异是否显著。双样本t检验用来检验两个样本的平均值与每个样本所代表的总体之间的差异是否显著。配对样本t检验用于检验两组匹配受试者获得的数据或同一组受试者在不同条件下获得的数据的差异,目的是消除混杂因素的影响。
3. 方差分析
方差分析(ANOVA)是一组被广泛应用于分析个体价值相对于群体平均值的变化的统计模型,如组内和组间的“差异”。观察到的某一个特定变量的方差被划分为可归因于不同变异源的变量。方差分析对于比较三组或更多组或变量的统计显著性非常有用。它在概念上类似于多个双样本t检验,但它更保守,导致的第一类误差更少,因此适用范围更广。
4. 相关性分析
相关分析是检验两个变量是否相关的一个简单而有用的单变量分析法。可以应用于:1,鉴定与一个已知生物标志物相似的特征;2,按照特定模式识别特征。支持的相似算法包括:欧几里得距离、皮尔逊相关、斯皮尔曼秩相关和肯德尔等级相关系数检验。
5. 火山图
火山图是一种散点图,通常用于展示RNA水平或其他组学实验的结果。火山图展示显示统计显着性(P值)与变化幅度(倍数变化)的关系。火山图可以快速视觉识别具有大倍数变化的基因,这些大倍数变化的基因在统计上往往也很重要。它们可能是生物学上最重要的基因。在火山图中,最上调的基因朝右,最下调的基因朝左,而统计上最重要的基因朝上。
多变量分析
代谢组学数据通常由许多特征(峰、化合物等)组成。许多特征随着时间、表型或不同实验条件的变化而变化。多变量数据分析(Multivariate Analysis, MVA)是分析代谢组学数据所需要的。常见的多变量分析包括:主成分分析、多元方差分析、多元回归分析、因子分析和判别分析等。
1. 主成分分析
主成分分析(Principal Component Analysis, PCA)是一种广泛使用的统计方法,它利用正交变换将一组观测到的令人信服的相关变量的观测值转换成一组称为主成分的线性不相关变量的值。这是一种无监督的统计分析方法,可能是代谢组学研究中使用最广泛的统计工具。PCA主要用于探索性数据分析和建立预测模型。
2. PLS-DA/OPLS-DA
偏最小二乘判别法分析(PLS-DA)是一种监督多变量统计分析方法。它在降维的同时结合了代谢物变化与实验分组的回归模型,并采用一定的判别阈值对回归结果进行判别分析。与主成分分析相比,PLS-DA分析可以进一步显示组间差异。正交偏最小二乘法判别分析(OPLS-DA)是一种多因变量到多自变量的回归建模方法。该方法的特点是可以去除自变量X中与分类变量Y无关的数据变化,使分类信息主要集中在一个主成分上。这使得模型简单易懂,主成分评分图的识别效果和可视化效果更为明显。
OPLS-DA可以过滤独立于实验条件的变化。因此,与PLS-DA相比OPLS-DA能更好地反映与实验条件有关的样品差异,并能更好地实现组间样品的分离。PLS-DA常用于比较两个或多个组,而OPLS-DA常用于比较两个组。此外,OPLS-DA比PLS-DA在筛选差异代谢物方面更准确。OPLS-DA产生的VIP值常用于筛选差异代谢物。
3. 树状图分析
树状图是显示对象之间的层次关系的图。树状图最通常是作为层次聚类的输出创建的。 树状图的主要用途是找出将对象分配给群集的最佳方法。
4. 热图分析
热图是统计数据的图形化表示,一个矩阵中包含的各个值用颜色表示。热图适用于显示多个变量之间的差异,显示是否存在彼此相似的变量,以及检测彼此之间是否存在相关性。
5. K均值聚类or自组织特征映射
K均值聚类(K-means Clustering)是一种矢量量化方法。K-means首先要估算出将要划分多少个类别,然后根据相似度的距离将所有基因放入这些类别中。K-means计算比层次聚类法小得多,而且更有效。自组织图self-organizing map (SOM)或自组织特征图self-organizing feature map (SOFM) 是一种人工神经网络,使用无监督学习对其进行训练,以生成低维(通常为二维)离散化表示训练样本的映射,因此是一种进行降维的方法。
与K-means不同,SOM的中心点之间存在一个拓扑顺序。在更新中心点时,相邻的中心点也将被更新,直到达到设定的阈值或中心点不再发生显著变化。最后,得到一系列隐式定义多个簇的中心点,并将距离该中心点最近的对象分类到同一个簇中。SOM强调簇中心点之间的邻近关系,相邻簇之间的相关性更强。SOM常用于可视化网络数据或基因表达数据。
相关服务
How to order?